
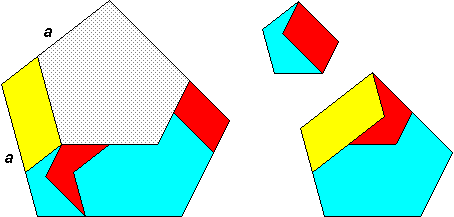
Hingeable regular pentagons of ratio 1 : 2 :: Ö5 ; 6 pieces
New dissections of diverse polygons
The following dissection of hingeable pentagons was published on the reader's page of Spektrum der Wissenschaft from January 1999, but I had not known what hingeable dissections are to that time.

Hingeable regular pentagons
of ratio 1 : 2 :: Ö5
; 6 pieces

Hinged pieces for pentagons
of ratio 1 : 2 :: Ö5
Unhingeable 6-piece dissections of
pentagons with ratio 1 : 2 : 2 :: 3
ó and the only necessity of one of
the angles having to be embraced by two sides of equal length. One of the
pieces has to be turned over though, unless there is a right angle involved.
Of course, if you split the larger parallelogram into two equal pieces,
you get a method that will work for any convex pentagons at all, - without
having to turn over any pieces!
Well, the following hingeable
dissection of two {8/2} ís to one is such an easily improved case.
Frederickson shows a 16-piece
solution with full rotational symmetrie (page 161 in Hinged Dissections:
Swinging and Twisting),
but if you break the symmetrie, you can find many solutions with 13 pieces.
I
decided to show a solution
that has as few small pieces as possible and almost the same number of
pieces for each of the {8/2}
ís. Another property is what I would call "smooth hinged". This means that
you have to swing any of
the hinged pieces only once and into one direction. For other hinged
dissections, it is often
neccessary to swing a piece into one direction first, in order to change
the position
of some other pieces, and
then swing that certain peace into the the other direction in order to
finally fit it
into the desired figur.
I would consider swinging more then once into the same direction as not
being
"smooth" either, - though
I do not know of such a case yet.
If the dissections are of
more than one polygon to another, then of course it is usually neccessary
to
preform translational moves
too. It should be said, that if it is not possible to swing hing the pieces
in a
non wobbly manner before
using such translational moves that require any of the pieces to cross
over
each other, - well then
from my opinion the dissection is wobbly hinged, no mater if the swinging
itself
can be don without wobbling!
There is no problem of that
kind for seperating the pieces of the smaller polygons out of the larger
polygons within the dissection
shown bellow. It can be done with one move for each of the smaller
polygons, but I donít know
if allowing only one translational move for the hinged polygons would make
sense as being another condition
for "smooth hinged" dissections.
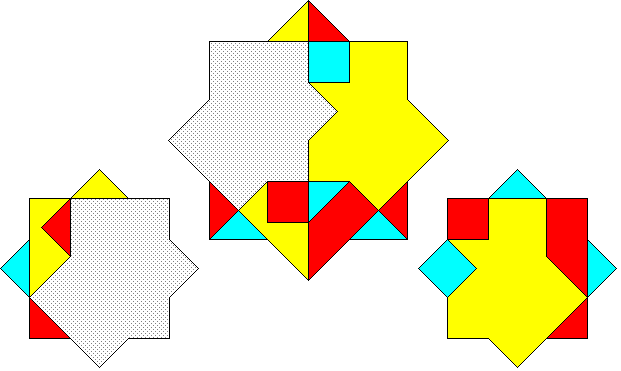
Hingeable two equal {8/2}
ís to one ; 13 pieces
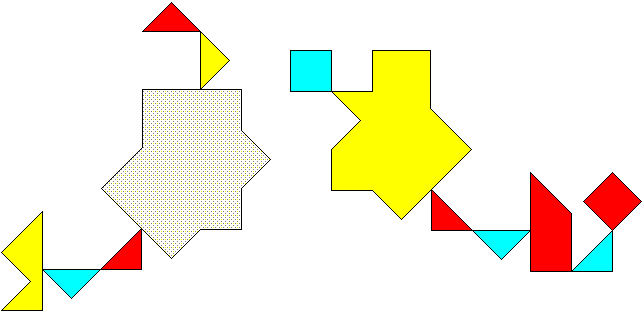
Hinges for two equal {8/2}
ís to one
The following dissection of four equal dodecagons to one is wobbly hinged, - although readers of Greg Frederickson's new book may not consider the dissection to be swing hinged, because Frederickson's definition of a triple hing does not allow any dissections with triple hinges to wobble (but why only allow wobbly hinged dissections with common double hinges?).

Hingeable four regular dodecagons
to one ; 19 pieces
It's not hard to find a 12-piece unhingeable dissection for regular dodecagons of ratio 1 : Ö2 :: Ö3 (Greg Frederickson told me that Evans Valens was the first to do so), but I don't know if one can do better than 17 pieces for a hingeable dissection.
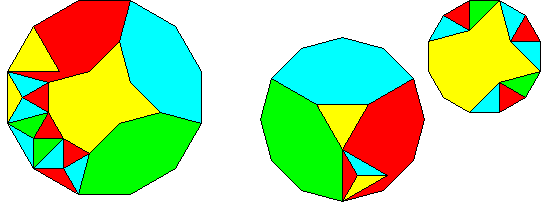
Hingeable regular dodecagons of ratio
1 : Ö2 :: Ö3
; 17 pieces