It
seems as if there are no special classes of hingeable three squares to
one existing that afford less than seven pieces, - so it is expectable
that there are more hingeable classes than the unhingeable ones. I know
of 7 classes of unhingeableI three squares to one, and I have found 14
classes with hingeable 7-piece dissections that have got the advantage
of using at least one piece less than required for their special relationships.
You will view only 13 classes on this webpage though, because Greg Frederickson
seems tohave
found the one that he names the Pythagoras-extended-twin class a bit earlier
than I have.
Additionally
I shall show all special cases of three hingeable squares with 6- piece
dissections that I know of and some rational 7-piece dissection that are
not already listed in Greg Fredericksons new book.
As
for the special classes of hingeable four squares to one, ó those with
two equal squares do not afford any more pieces than the special classes
of hingeable three squares to one. Thus I shall show a few 7-piece (hingeable)
classes and two new 6-piece classes of unhingeable four squares to one.
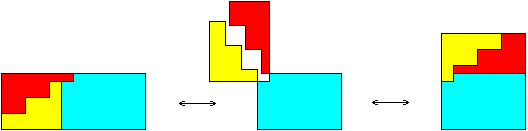
First
though, I would like to show how the second variant of the T-step is applied
to rectangles:

The
shown example is a 7a ´
12b - rectangle, that is hingeably dissected into a 12a ´
7b - rectangle. The same principal technique converts parallelograms with
(2n + 1)a ´
4nb to such with 4na ´
(2n + 1)b or versewise. For the following classes of squares you
will additionaly see the application of the Q-step to rectangles (instead
of trapezoids, as you may be used to), - but since Frederickson shows that
technique in his new book, I canít show this kind of Q-step for itself
on this webpage.
1.
Rational classes and special cases of hingeable squares
There
is a class of hingeable three squares to one with an interesting relation
to Cossaliís class. If you take (2a)² + (2a + 4)² + (a²
+ 2a)² = (a² + 2a+ 4)², then when
a is even, you get Cossaliís class (times four), and every odd integer
leads to what I call the Cossali-twin class. It yields 7-piece dissections
that are made hingeable by using two Q-steps.
10²
+ 14² + 35² = 39²
; (4a - 2)² + (4a + 2)² +
(4a² - 1)² = (4a² + 3)²
There
is another class of hingeable three squares to one that derives from the
same relationship as the Cossali-twin class. It uses both a Q-step and
a T-step, being the only class with that property that I know of.
I thus call it the QT-step class:

15²
+ 24² + 40² = 49²
; (4a²
- 1)² + (8a² - 4a)² + (8a²
+ 4a)² = (12a² + 1)²
Since
the size relation between the sidelengths of the y-square and the x-square
approximates 9 : 2 for the following class, I call it the square-sum-extended
class (for hingeable squares), - considering that the other square-sum
classes approximate a relation of only 2 : 1 (see page 84 and 85 in Dissections
Plane & Fancy). It uses a T-step for dissecting the z-square.
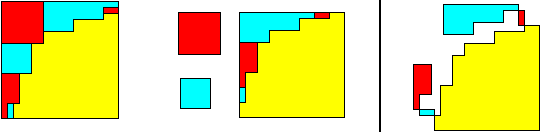
The following class of hingeable three squares to one has got two exceptional
abilities that the other classes do not have. First, although the sizes
of the squares are all rational, it seems unavoidable to use a T-slide.
This will always lead to a nonorthogonal line with exactly 45º inside
of the w- or y-square. Second, all dissections are wobbly hinged, - so
I decided to call this the wh-square class. Of course I am aware
that I would have to change that name if someone should find any nonwobbly
hinged solutions (or any other wobbly hinged classes of squares).
The principal technique is to use a T-step in order to get a y
´(y-x)-
rectangle (attached to a thin (x ´
y)-rectangle) after the x-square and the y-square have been taken out of
the area of the w-square. Then a T-slide gives that rectangle the proportions
necessary to make it fit into the y-square.
The 7-sided yellow piece top left could be defined as the "union" of
a piece from the T-slide and a piece from the T-step, because "both" pieces
(would) share an anchor point.
18²
+ 49² + 42² = 67²
, (2(2a + 1)²)²
+ ((6a + 1)²)² + (24a² + 16a + 2)²
= (44a² + 20a + 3)²
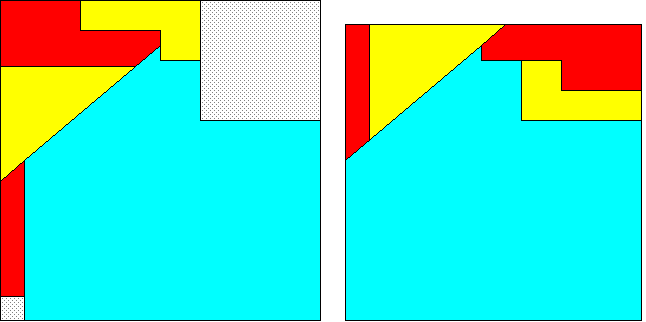
The
odd solutions of the PP-plus class yield hingeable 7-piece dissections
of squares, to which two Q-steps are applied. Take the x-square out
of the upper right corner of the w-square, and the first step transforms
the remaining area into a rectangle. Then take out the z-square, and the
second Q-step transforms the remaining area into the y-square.
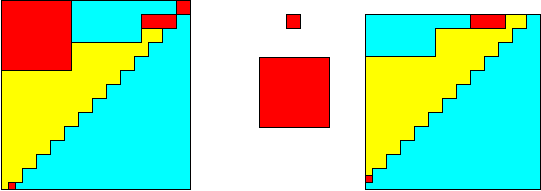
2² + 10² + 25² =
27²
Hinges for 2² + 10² +
25² = 27²
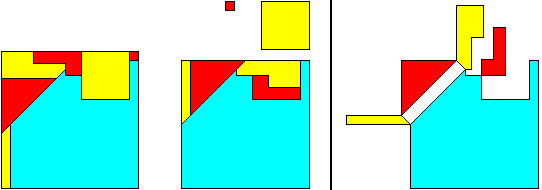
137²
= 128² + 48² + 9²
The
following solution belongs to a class of usually unhingeable 6-piece dissections,
because the smallest square has to be dissected with a common step-technique
(which is only hingeable for this special case). It should be mentioned
that the unhingeable 6-piece dissections still require one piece less than
those of the the special relationship to which they refer ( 2(w - y) =
z ).
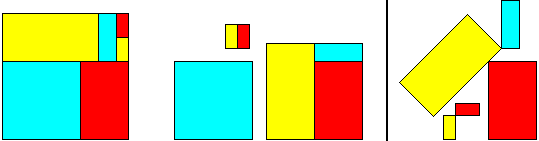
Hingeable
squares of ratio 4 : 13 : 16 :: 21 ;
6 pieces
Of
course, there are two 7-piece classes of hingeable squares that can be
derived from the same extension of the relationship by using either a Q-step
or a T-step for the dissections of the x-square. Since the z-square is
always split exactly in the midst, I call these classes the split-square
classes, - one being the split-square-Q- and the other the split-square-T
class.
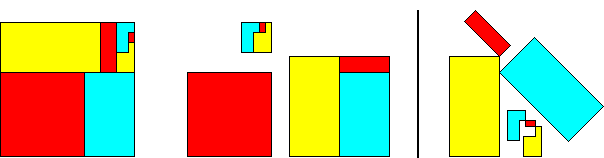
67²
= 50² + 42² + 15²
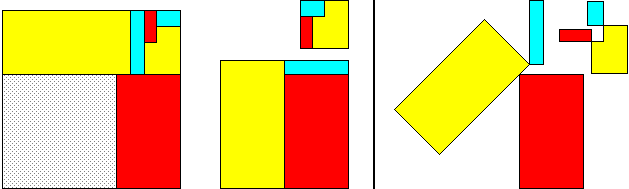
89²
= 64² + 57² + 24²
If
the x-squares are required to be even smaller, then there are two classes
of hingeable squares that derive from special cases of the relationship.
Thus, just as for the other two classes shown above, a Q-slide is converted
to a Q-step and a T-slide to a T-step. This leads to what I call the split-square-extended-Q
class and the split-square-extended-T class.
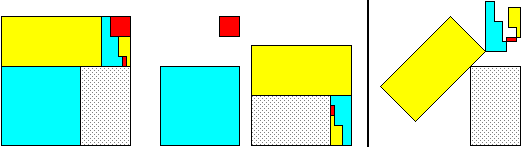
129²
= 100² + 79² + 20²

81² = 64² + 49² + 8²
Note
the existence of another class of unhingeable 6-piece dissections that
derives from the same extension of the relationship by converting a P-slide
to a step.
The
odd solutions of the square-sum-minus class yield hingeable dissections
that can be dissected in two totally different ways. One method uses a
Q-step, and the other affords two T-steps. The first method suggests a
somewhat different solution than the one I gave for dissecting the squares
of relationship x + y = w within the range of sizes
for 2x < y < 8x .
Due
to the existence of hingeable 7-piece dissections for y < 2.5x
, only the first four solutions of this "class" afford less pieces than
the more general dissections of the special relationship. All the others
have only got the advantage of all lines being parallel to the boundaries
(there are more "classes" of that kind). Since there is a (simple) hingeable
6-piece dissection for the first solution (see Hinged Dissections: Swinging
and Twisting), I decided to show the second solution in sense of that
it is a special case of a hingeable 7-piece dissection.
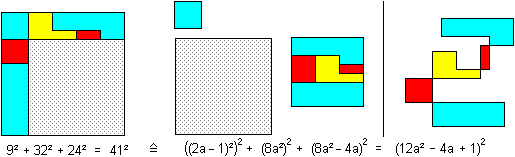
first
method

9²
+ 32² + 24² = 41²
; second method
Robert
Reid found an unhingeable 5-piece solution for the following three squares
to one (figure 8.17, page 86 in Dissections Plane & Fancy ),
and I would like to show a hingeable 7-piece solution:
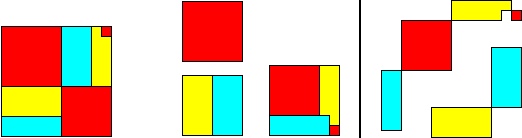
Hingeable
squares of ratio 6 : 6 : 7 :: 11 ;
7 pieces
The
following special case of three hingeable squares to one has got the (relatively)
largest equal squares that I know of (if you ask for 7-piece dissections):
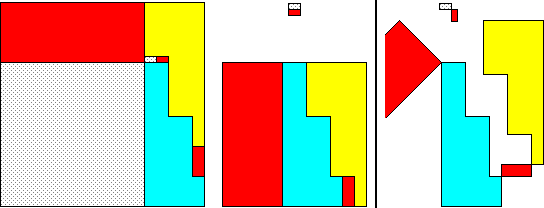
Hingeable
squares of ratio 12 :12 : 1 :: 17 ;
7 pieces
There
are quite a few 8-piece classes of hingeable squares existing that do afford
one piece less than the dissections of their special relationship, - considering
that some of the extended cases can not be dissected with less then 9 pieces!
Exceptionally I shall show one of these 8-piece classes, because it has
also got the advantage of all lines being parallel to the boundaries.
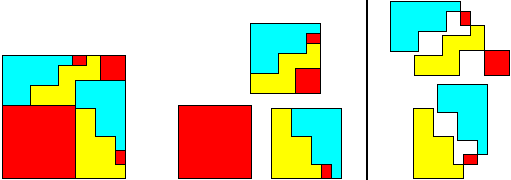
123²
= 70² + 70² + 73²
I
know of a class of unhingeable four squares to one that is so simple, that
I donít quite believe I could have been the first to discover it:
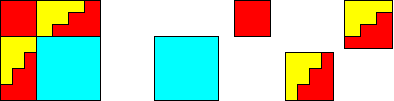
25²
= 9² + 12² + 12²
+ 16²
Another
unhingeable 6-piece class is (2a²)² + (2a²)²
+ (2a² + 2a)² + (2a² + 2a + 1)² = (4a²
+ 2a + 1)², for which I show the case a = 3 :
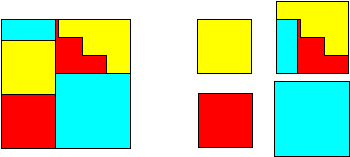
43²
= 18² + 18²
+ 24² + 25²
Of
course, using a P-slide instead of steps yields 7-piece dissections for
an unhingeable special relationship of four squares to one. It is
x = y and x + z = v , with v > 2x . If a T-slide
is applied, you get a special relationship of hingeable 8-piece dissections.
Now convert the T-slide to a step (for certain squares), and you get at
class of hingeable four squares to one:
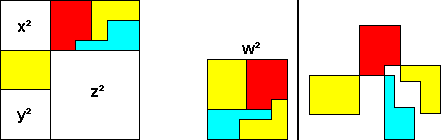
50²
+ 50² + 80² + 89² = 139²
, (2(2a+1)²)² + (2(2a+1)²)² + (16a²+8a)²
+ (20a²+4a+1)² = (28a²+12a+3)²
Using
a Q-step leads to another class of hingeable 7-piece dissections (but no
8-piece dissections for the relationship when a Q-slide is applied!).
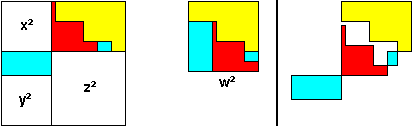
25²
+ 25² + 35² + 37² =
62² , ((2a - 1)²)² + ((2a
- 1)²)² + (4a² - 1)² + (4a² + 1)²
= (8a² - 4a + 2)²
The
case v < 2x yields another unhingeable class of 6-piece dissections
plus two hingeable classes of 7-piece dissections. Again a common step
is applied for the unhingeable class, and using either a Q-step or a T-step
leads to the hingeable classes. It should be mentioned that both a Q-slide
and a T-slide yield 8-piece dissections for the special relationship.
The
following figure shows only the systematic structure of all three classes,
- regardless of the sizes that the squares should have for any special
case.

2.
Irrational classes and special cases of hingeable squares
There
seem to be no irrational sizes for the 5-piece classes of three squares
to one, - but the situation changes if you ask for the 7-piece classes
of hingeable squares. The 14 classes that I have found split into 10 classes
of (only) rational sizes and 4 classes of such a kind as that some of the
size relations between the squares are irrational.
In
New dissections to the special relationships of squares I had mentioned
an alternative solution for the hingeable dissections of squares with
y = x(w - x) and 5x < w , and that it
leads to a hingeable class. For the dissections of the relationship, take
the x-square and the y-square out of the upper corners of the w-square,
and then use a T-slide in order to get a rectangle of size w ´
(w-x) . For the dissections of the class, that T-slide can be converted
to a T-step. Then use a T-stripe in order to dissect the rectangle into
a square.

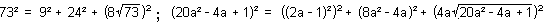
The next largest case after the one shown above has got only rational
squares: 169² = 25² + 60²
+ 156²
In fact, the solutions described by the formula above even include
a whole special class with only rational
squares, - next to the infinite larger number of solutions for which
the the z-square would have an irrational
side-lenght relation to the other squares.
The rational solutions described by the formula above can be determined
by using
 ,
,
- but every third solution of this formula is not integer and thus
wrong in sense as that there are no
hingeable 7-piece dissections for those cases!
For solutions twice the size from the formula above, an integer sequenz
can be build by using the following
algorithm: Multiply a with a constant factor of 7; then
subtract from that product 1 and the next smaller a in
the row in order to get the next larger a:
an+1
=
7an -
an-1 - 1
Note in German for mathematicially interested readers of my webpages:

A
special case of this class (for a = ¥)
leads to a 6-piece dissection:
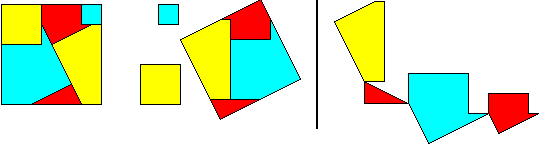
Hingeable
squares of ratio 1 : 2 : 2Ö5
:: 5 ; 6 pieces
As already mentioned, my hingeable solution for the special relationship
of squares with y = z and x > Ö2y
yields a class of 7-piece dissections, - though I use a T-stripe instead
of the second T-slide as shown for the dissections of the relationship
(because the T-stripe is easier to draw).
I had also mentioned that the the T-slide could have a different orientation
within the w-square (for the dissections of the special relationship).
This would reduce the range of sizes for the relationship, but it yields
another class of hingeable squares (by converting the T-slide to a T-step
, - again I use T-stripe instead of a second T-slid as shown for the dissections
of the relationship).
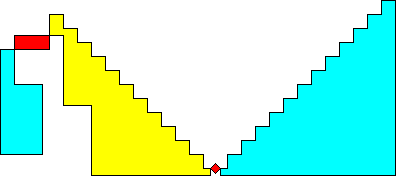
Again
there is a special case (for a = ¥)
that requires only 6 pieces: The following special class of squares is so irrational that only z
and w have a rational relation that allows the application of a T-step.
This class is a conversion of my extended solution for
A special case of this class (for a = ¥)
requires only 6 pieces:
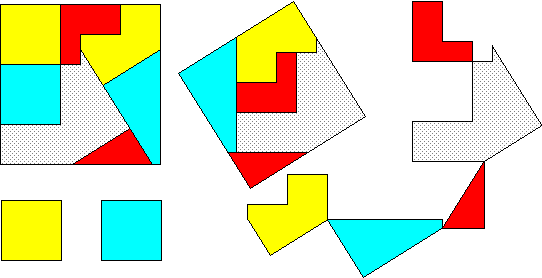
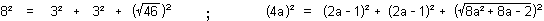
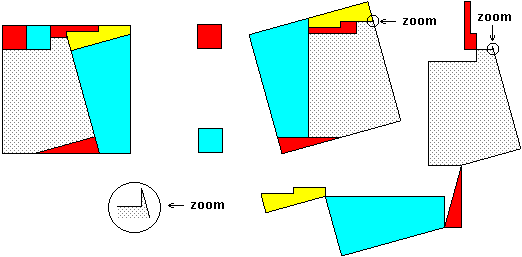
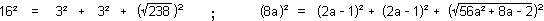
Hingeable
squares of ratio 1 : 1 : Ö14
:: 4 ; 6 pieces
x + y = w with y >
(3 + 2Ö2)x.
![]()
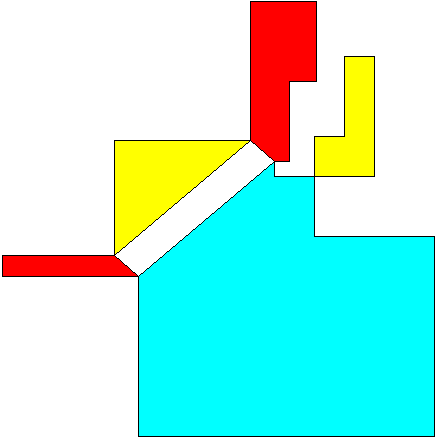
Hinges for 16² =
(8 - Ö46)² +
6² + (8 + Ö46)²
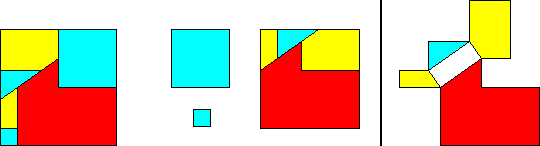
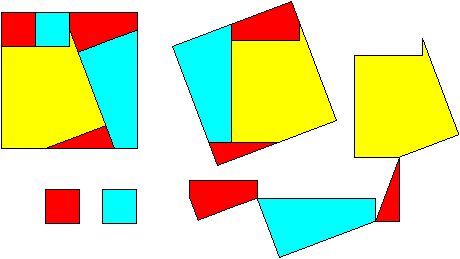
Hingeable squares of ratio (2 - Ö2)
: 2 : (2 + Ö2)
:: 4 ; 6 pieces