n =2 n = 3
The
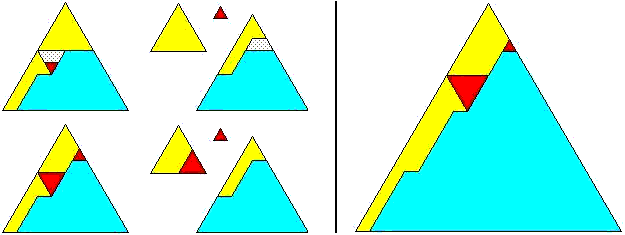
first shown case can be dissected hingeable without using more pieces than
required for unhingeable dissection of the class:
In
Dissections: Swinging and Twisting this kind of dissection is called "wobbly
hinged", because certain pieces can not swing from one position to the
other without crossing each other at least partwise. The
odd solutions of the square-sum-plus class are a hingeable 5-piececlass
of triangles (compare unhingeable solution of figure 9.13, page 96 in Dissections
Plane & Fancy ). It
should be mentioned that there is something like an unhingeable variant
of the T-step, and it can be applied to the even solutions of the square-sum-plus
class. What’s interesting is that fewer lines have to be cut out of the
z-triangles as for the comparable dissections that use the common step
technique (figure 9.13,page 96 in Dissections Plane & Fancy).
86²
= 36² + 50² + 60²
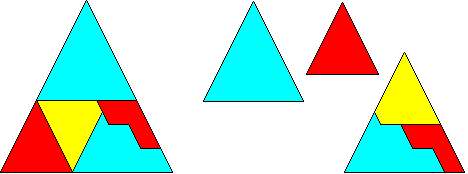
The
PP-double class for triangles splits into two classes if you ask for hingeable
dissections (from my opinion there would be two classes for the unhinged
solutions too). I you use (n²+2)² = (2n)²
+ (2n)² +(n²-2)² in order to describe both classes,
then a "hidden" Q-step dissects the odd solutions, and a hidden T-step
will do for the even solutions. Unfortunately all solutions are wobbly
hinged! The
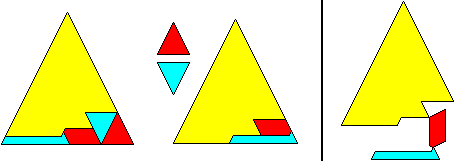
Cossali-twin class (see New dissections to the classes of squares) yields
hingeable 5-piece dissections of triangles. The
following class of four hingeable triangles to one is related in the same
way to the class for which David Collison gave 5-piece dissections (page96
in Dissections Plane & Fancy ) as the Cossali-twin class is related
to Cossali's class. There
is a formula that can be used to describe a numerical class that splits
into two differently dissected classes of four hingeable triangles to one:
(2n² + 2n + 2)² = (n²)² + (n²)²
+ (n² + 2n)² + (n² + 2n+ 2)². Again the odd solutions
use a Q-step and a T-step is applied to the even solutions.
Hingeable
triangles of ratio 1 : 4 : 8 :: 9 ; 5 pieces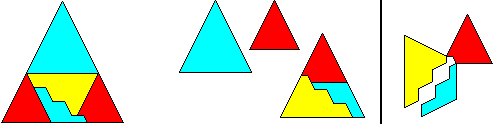
121² =
72² + 49² +84² ; (12n²+4n+1)² =
(8n²)² + ((2n+1)²)² + (4n(2n+1))²

27²
= 10² + 10² + 23²
66²
= 16² + 16² + 62²
39²
= 10² + 14² + 35² ; (4a² + 3)²
= (4a -2)² + (4a + 2)² + (4a² - 1)²
29² =
4² + 10² +10² + 25² ; (n² + 4)²
= 4² + (2n)² + (2n)² + (n²)²

26²
= 9² + 9² + 15² + 17²

86²
= 36² + 36² + 48² + 50²