17² = 8² + 15²
Corrections and a new order to certain triangle classes
Most of the following dissections are listed only with short explanations, - but for the classes of two triangles to two, I must make an exception. The reason is, - Iím sorry to say this - that Greg Frederickson doesnít seem to have enough time to analyse the vast experiences that he has made with dissections, - or otherwise he probably wouldnít have gotten some things mixed up as he did for the following triangle-classes that refer to his books Dissections Plane & Fancy and Dissections too! Swinginí.
Of course, giving order to the new classes (and the old ones) is also a matter of taste. For instance: I consider a method for dissecting the classes of polygons as being always exactly the same method for a certain number of pieces, - and to have only such "variants" in sense of that the any of the uncut original polygons may have different positions within the rearrangements (after the transformations), - whereas those certain number of pieces always derive from the same cutting-method (Iíll explain that closer with the examples to come). Thus some of the variants that Frederickson considers to belong to one method do not fit into this schema, - and on the other hand, I have good reasons for the way I order the classes of two triangles to two that include Fredericksons old classes (and more).
To begin with, there is a formula that can be used to describe both Pythagoras's and Plato's class:
(n² + 1)² = (2n)² + (n² - 1)²
When n is odd you get Pythagoras's
class (times two), and if n is even you get Plato's class. Frederickson
combines both classes to what he calls the PP-class, and describes a method
that is supposed to work for all triangles of that class. Something got
mixed up in his book though, because the flip-up technique as described
on page 92 in Dissections Plane & Fancy does not work if n is odd.
Instead, It is the flip-down technique that works for the entire PP-class,
though it seems that David Collison only used it for dissecting the triangles
of Pythagoras's class. As an example that it works for Plato's class as
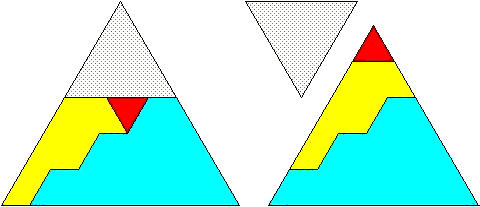
well, I shall show the case 17² = 8² + 15² :

17² = 8² + 15²
The shown triangles are equilateral, but since all dissection-methods that refer to classes and special relationships will work for any kind of triangles, - and because certain scalene triangles are easier to draw on a bitmap than the equilateral ones, - the following graphics will show such triangles from now on.
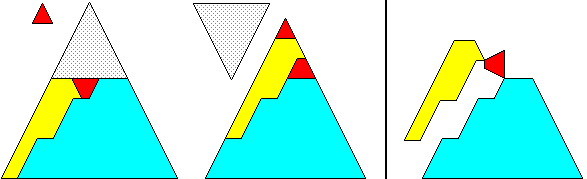
If you ask for hingeable dissections, then the flip-up technique yields hingeable triangles only for Plato's class. In order to make Pythagoras's class hingeable, it seems that it is unavoidable to use a new type of technique that transforms a trapezoid to a triangle. By studying Anton Hanegraaf's T-slide technique, I found out that one kind of T-slide that he had found can be converted to a step-dissection that saves one piece compared to the slide. I immediately send my first dissections that used that new technique to Greg Frederickson, who responded by letting me know that it would be better not to follow up with sending him any further dissections for a while. Two months later he then send me his more generalised version of a technique that he called the "T-step" (a name to which I fully agree, - though there is still another kind of T-step-like technique existing). He had never shown me any special dissections where it is used though, - and most of all, it seems that he was not aware of how general the technique really is! This is Hanegraaf's T-slide applied to trapezoids, and the dotted line (not belonging to the slide) shows how a T-step can be derived from a T-slide:

This is the T-step that emerges from the figure above, and the left part of the graphic shows how the three pieces are hinged together:

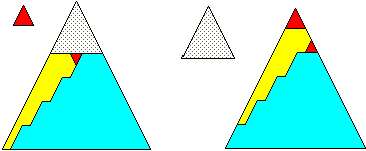
If you consider the bottom line of a trapezoid to be the longer of the two parallel lines, than of course both trapezoids have the same orientation. There is a line inside of the first trapezoid (left) that touches the trapezoids top line and that must also touch a line of the step exactly on the middle of the step's line. This meeting-point inside the trapezoid must always stay the same, - no matter what slant the line running from above has got. But the line running from above does not necessarily have to touch the top-line of the trapezoid. If it touches the top left vertex, then the transformation will lead to a triangle. But it can even touch the left outside line of the trapezoid, and then the transformation will lead to a trapezoid with a different orientation of it's parallel lines:

I had shown Greg Frederickson one triangle- and a few square-dissections using the T-step, before he gave me his reply not to follow up with any further material for a while. I grant him as being the first to discover that the two trapezoids must have only one angle in common, - because I did not need that property for my dissections, and was thus not aware of it.
In a letter that contained a permission form for showing some of my dissections in his new book, Greg Frederickson had acknowledged me as having discovered the T-step (he himself had known only a 4-piece step until then, which I had not seen before!)). Now he has the nerve to show the technique in his book as if it where his discovery, - without even mentioning my name!
Surely the triangle-dissections that I had sent Frederickson later (being the last ones he wanted to see) where unavoidable to be found, - and they use the first shown version of the T-step, though they have more angles in common than necessary for the more general step (the first triangle-dissection that I had found can be considered as a special case of both versions).
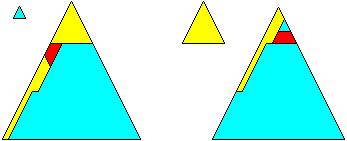
The first kind of T-step affords trapezoids that have a height-ratio of two consecutive integers. This is an important different quality compared to a Q-step, because a "common" Q-step affords a height-ratio of two consecutive odd integers for the trapezoids. As Frederickson showed in his first book, the Q-step can be used two dissect the triangle of Platoís class. It will not work for Paythagorasís class, because the height-ratios of the trapezoids are those of two consecutive integers. Thus the T-step is suitable instead.
If you substitute n´ = 2n + 1 for the even solutions within the formula of the PP-class, and divide by a common factor of two, you get a formula only for Pythagoras's class. Since the hingeable dissections of that class have a slightly different appearance depending if n is even or odd (as do all triangle-classes using the T-step) , I shall show an example for each case:
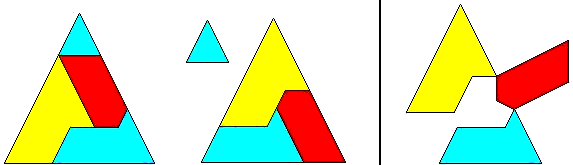
25² = 7² + 24²
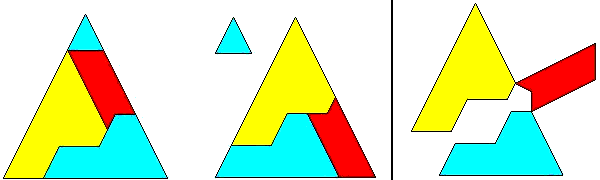
41² = 9² + 40²
Readers of the book Hinged Dissections: Swinging and Twisting might notice something peculiar when they compare figure 5.2 on page 49 with my triangles of the Pythagoras class. It could appear as if I had seen Fredericksonís second dissection of two hingeable triangles to one, before getting the idea of using the T-step as a conversion of Fredericksonís application of Hanegraafís more general technique. This is not the case, because to that time I had even asked Frederickson if he would have discovered any new triangle dissections (in the meantime), before sending him my solutions for the triangles of Pythagorasís class, - and he had only known one hingeable solution for the general case until then (and I should say that I had already shown him a new dissection for the general case that takes use of a T-stripe, - so why bother to mention that generalizing the T-step of Pythagorasís class would yield another hingeable solution, since I was urged to slow down the information process to that time anyway).
So if you should have that
book and take a look at figure 5.2 again, then notice that there are at
least three solutions existing, and Frederickson was only aware of one
(figure 5.1) before taking up the correspondence with me (and seeing my
triangles of the Pythagoras class). Obviously he now gives statement as
if he would only know the second solution, though I had sent him a third
and not found it necessary to mention that obvious second solution, since,
- for instance, both have a shorter size extension than the solution that
takes advantage of a Q-step.
On page 94 of his book Dissections Plane & Fancy Greg Frederickson shows two different methods (actually three) in order to dissect two different classes of two triangles to two. After finding out that the Plato-extended class was contained in the Pythagoras-extended class, Frederickson decided to restrict the Pythagoras-extended solutions to n = m + 1 (see "Updates" to chapter 9 on Fredericksonís homepage). In that case you would have to restrict the Plato-extended solutions such as that m is only even, or again the classes would get mixed up!
Judging from the content of his second book, Frederickson was not aware of that fact (I had already prepared a letter dealing with it, but could not send it off anymore). He applies Method 8 (page 94, figure 9.10 in Dissections Plane & Fancy) to certain solutions of his old Pythagoras-extended class, and now regards them to belong to Platoís-extended class instead. This could even be considered as even twice wrong (In a certain sense), because, - as you will see - the Pythagoras-extended solutions of page 94 can be dissected with only one method (I really mean one), and the "variant" of method 8 as shown in figure 9.10 actually works for still another class to be shown.
The problem is though, that the formulas given for the classes of page 94 will not generate all possible quadruples of triangles that can be dissected with those methods.
As an example take 89² + 33² = 63² + 71², which can be produced by using Fibonacciís formula for m = 16; n = 3; p = 5; and q = 3. It can not be produced with n = 1, (according to Frederickson the limiting fact to the Plato-extended class), even if you allow p and q to be not necessarily integer as suggested in Fredericksonís second book, - and of course even if the sizes are only required to have the same given proportions to each other, regardless of the absolute size. Yet, - Method 9 (page 94 in Dissections Plane & Fancy) still works for dissecting such triangles!
Actually even Fibonnaciís formula will not even yield all possible sizes, unless m is allowed to be a non integer variable (and even irrational). The problem is that, - instead of using Fibonacciís formula in order to find a numerical class that yields suitable sizes for the triangles, - the other way around seems to be the better approach. In that case you will get a formula with only two variables, which of course can be derived from Fibonacciís formula too, - but that would afford quite a lot of unnecessary algebraic work!
For anybody who would like to try the deduction of only two variables by using Fibonacciís formula: the real limiting fact to Pythagorasís extended class (referring to method 8 from Dissections Plane & Fancy) is the ratio between q and p, which has to be that of two consecutive integers (so you can stick to p an q as being integer), - and for the extended class of Plato (referring to method 9) the ratio must be that of two consecutive odd integers.
All the classes of two triangles to two that I know of can be described by using only one formula:
if x² + y² = z² + w²
than x = n² + (n + 1)p + 1; y = |(n - 1)p|; z = n² + (n - 1)p - 1; w = 2n + (n + 1)p
Of the two variables only n is provided to be integer, and p is even allowed to be negative. This leads four hingeable classes, - or two classes with two subclasses each -, depending whether n is even or odd and whether p is positive or negative.
This formula can easily be deducted from the formula of the PP-class by letting (n + 1)p be the additional or the missing length of any given trapezoid compared to such trapezoids of the same height that can be transformed to the triangles of the PP-class. The figures below require (n + 1)p and (n - 1)p to be absolute values, and the left figure refers to p being negative.
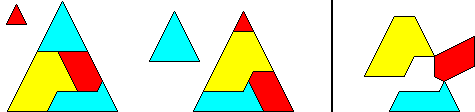
For the first case let n be odd and p be positive. Since this leads to a ratio of two consecutive integers for the trapezoids, they can be transformed with the help of a T-step. I shall call this class the Pythagoras-extended-plus class.
For my opinion, a class (of dissections) is defined by the method of itís dissections, - and not merely by a numerical formula. Using two quite different methods thus means that you are dealing with two different classes, as long as there isnít any other method that combines both of them (or obviously, you could combine the classes as you like). From this point of view it should be said, that the first "variant" of method 8 as shown in figure 9.9 of Dissections Plane & Fancy works for the entire Pythagoras-extended-plus class (that includes Fredericksonís old class), - so note the existence of both a hingeable and an unhingeable method for the triangles of this class!
As an example for the method that produces hingeable dissections, I show 10² + 5² = 11² + 2² (compare page 93 and 94 in Dissections Plane & Fancy), which refers to n = 7 and p = 2 and a division by a common factor of 6.
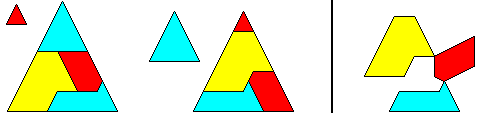
11² + 2² =
10² + 5²
If n is odd and p is required to be negative, then the ratio of the trapezoids changes in a quite dramatic way. Now it can have any value larger than 1 and smaller than that of two certain consecutive integers, but of course there is only one set of triangles for each possible ratio (referring to the same n). Note that the ratios can even have an irrational value!
The second version of the T-step will work for all triangles of this class, and I shall call it the Pythagoras extended-minus class.
If you ask for trapezoids that do not
have the ratios of consecutive integers, then itís not so easy to avoid
a small triangle, - provided the solutions are not to large for a crude
bitmap. The best example I could come up with is 188²
+ 9² = 183² + 44²
, which refers to n = 7 and p = -0.375 (multiply
the entire equation in order to get integers).

188² + 9²
= 183² +
44²
If n is even and p is positive, then
you get a ratio of two consecutive odd integers, - and for that case the
Q-step dissection that Frederickson shows for method 9 on page 94 is suitable.
I call this the Plato-extended-plus class. Since I can not expect that
anyone who would read my webpage has the possibility to read Fredericksonís
book too, I shall show the application of method
9 for the case 44²
+ 5² = 40² + 19²
, which refers to n = 6 and p = 1 .
44² + 5²
= 40² +
19²
If n is even and p is negative, any ratio larger than 1 and smaller than that of two certain consecutive and odd integers can occur. A variant of the Q-step will work for the dissections of that class. Frederickson used it in order to dissect certain triangles of his Pythagoras-extended class (page 94, figure 9.10), - but off course there is only one such case for every integer of n, whereas for each n an infinite amount of triangles can be dissected with the same method. It works for trapezoids that have a top-length smaller than that of the trapezoids of Platoís class (with the same height). I thus call this the Plato-extended-minus class, and show as an example 164² + 15² = 160² + 39² , which refers to n = 6 and p = 0.6 (again a somewhat eccentric solution because of the size-problem with the bitmap).

164² + 15² =
160² + 39²
Obviously there are no solutions of the Pythagoras/Plato-extended-plus classes existing that would belong to both classes, ó the ratios of the trapezoids are simply incompatible! The situation changes though, if you compare the solutions of the plus-classes with those of the minus-classes. When Frederickson used what he considers to be a variant of method 8 for dissecting certain triangles (figure 8.4 of method Plato-SE in his new book), he was of course not aware that his method works for an infinite larger amount of solutions - but some of them have got consecutive ratios for the trapezoids, so that they can also be dissected with the methods of the plus-classes!
Of course, the plus-classes are infinite larger as the comparable classes of Fredericksons book, but the ratios of the trapezoids are always the same. So the second variant of method 8 (from the old book) only works for an infinite smaller number of triangles, compared to those that can be dissected with the first variant.
As you can see, I use Fredericksonís first variant of method 8 to dissect what I call the Pythagoras-extended-minus class, - and it contains an infinite larger number of triangles than any of Fredericksonís classes. Still each minus-class has got infinite many solutions of which each corresponds to exactly one solution of the plus-classes. Additionally there are corresponding pairs of solutions existing that belong to only one of the plus-classes, - and, interesting enough, there are also corresponding solutions between the two minus-classes. There are no triples though, because the corresponding solutions of the minus-classes do not have the ratios as afforded for the trapezoids of the plus-classes.
As already said, Fredericksonís first variant of method 8 works for the entire Pythagoras-extended-plus class. The triangles of figure 9.10 (page 94 in Dissections Plane & Fancy) are a good example, and they refer to n = 9 and p = 5/3 when using the formula I gave.
37² + 5² =
35² + 13²
Actually, a variant of this method will even work for the Pythagoras-extended-minus class. Of course, it will produce only unhingeable dissections, as for 23² + 2² = 22² + 7², which refers to n = 5 and p = -½ .
23² + 2² =
22² + 7²
This is a good example of how one method for dissecting polygons produces two different variants in order to fulfil a greater rang of sizes.
As you can tell, the cutting-method for each of the variants leads to three certain pieces, - and those pieces will always change there relative position to each other in the same way after being rearranged within the w-triangle. Only the position of the small uncut triangle differs from the first to the second variant.
The first variant of the dissection-method works for the Pythagoras-extended-plus class, and the uncut triangle sites on top of the yellow colored step-piece within the w-triangle. The second variant is applied to the Pythagoras-extended-minus class, and the uncut triangle sites on top of the small trapezoid-shaped piece (red), that can be compared with the small triangle-shaped piece of the first variant.
In sense of unhingeable dissections,
this method can thus be applied to what I would call the Pythagoras-extended
class. It is not at all comparable with Fredericksonís class referring
to the same name, since it includes both the triangles of the minus- and
the plus-class. In his second book, Frederickson regards certain solutions
of the Pythagoras-extended-plus class to belong to his Plato-extended class,
- so his definition of the Pythagoras-extended class refers only to very
special cases of the class that I have defined.
This leads to the question if there is a single method for dissecting all the shown classes of two triangles to two?
Well, - since the flip-down technique works for the entire PP-class, the same principal kind of technique can be varied in order to achieve unhingeable dissections for the triangles of all the classes I gave. This union of classes could be named the PP-extended class, - but there is a size-restriction of (n-3)p £ 2 , because the unit method will not work for the entire rang of sizes that can be dissected with the special methods that I have already shown for the subclasses.
As an example of how the unit method works if p is positive, I shall show the case 22² + 3² = 18² + 13² , which refers to n = 4 and p = 1 (compare page 94, figure 9.11 in Dissections Plane & Fancy).
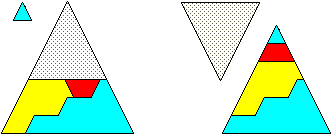
22² + 3² =
18² + 13²
There is no restriction to the unit method when using it for dissecting the triangles of the minus-classes, because such a "restriction" would be reached for triangles of equal size (p = -1). As an example, compare the unit method for 23² + 2² = 22² + 7² to the method shown further above, which only works for the Pythagoras-extended class.
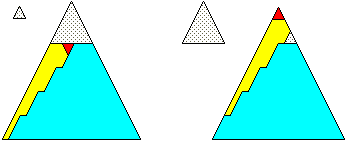
23² + 2² =
22² + 7²
Of course, this special case can also be dissected with the first variant of the method for Pythagorasís extended class. Whatís even more: in that case there seems to be no difference between both solutions, - but thatís why I gave the two small triangles of equal size a different color! Compared to the unhingeable solution that refers to the Pythagoras-extended-plus class, the two small triangles are exchanged within the shown solution that refers to the PP-extended-minus class.
I end these expositions about the classes
of two triangles to two with a little riddle: There are at least
how many differently dissected solutions existing for the case 23²
+ 2² = 22² + 7²
, and what are the sizes of n and p referring to the Pythagoras-extended-plus
class?